SIMD简介
在深度学习中经常会涉及到向量和矩阵运算,在之前实现的算子中通常会采用循环或者开源的向量运算加速库来提高计算效率,例如openmp、EIGEN、MKL等等。这些库的底层除了利用处理器的并行化能力,还会调用指令集优化代码。这里的指令集优化,大多数使用的是SIMD指令。
SIMD(Single Instruction Multiple Data)即单指令流多数据流,是一种采用一个控制器来控制多个处理器,同时对一组数据(又称“数据向量”)中的每一个分别执行相同的操作从而实现空间上的并行性的技术。简单来说就是一个指令能够同时处理多个数据。非常适合数据密集型的运算。
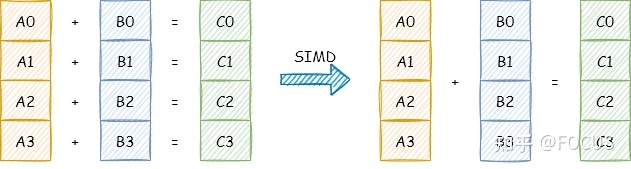
如上图所示:
- 一个普通加法指令,一次只能对两个数执行一个加法操作。
- 一个 SIMD 加法指令,一次可以对两个数组(向量)执行加法操作。
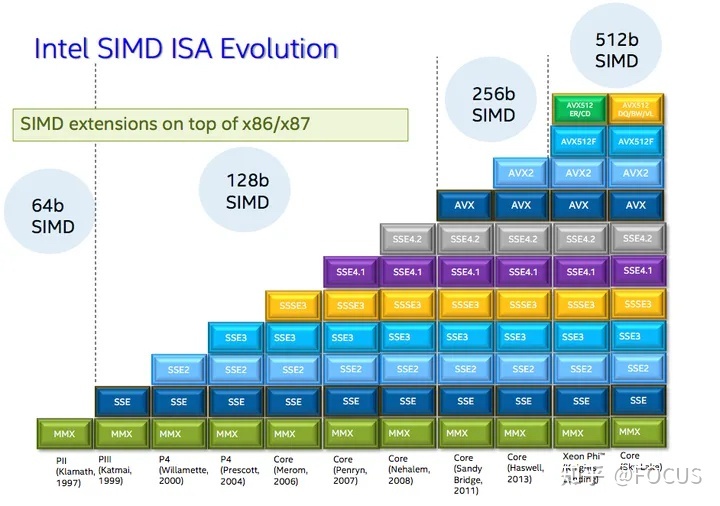

由上图可知,最简单的方法是使用Intel的跨平台库IPP或者使用MKL,但是可控性较差;最复杂的是直接使用汇编操作寄存器。本文通过内置函数(intrinsics)的方式使用SIMD指令。
SSE/AVX Intrinsics介绍
头文件
SSE/AVX指令主要定义于以下一些头文件中:
- < xmmintrin.h > : SSE, 支持同时对4个32位单精度浮点数的操作。
- < emmintrin.h > : SSE 2, 支持同时对2个64位双精度浮点数的操作。
- < pmmintrin.h > : SSE 3, 支持对SIMD寄存器的水平操作(horizontal operation),如hadd, hsub等…。
- < tmmintrin.h > : SSSE 3, 增加了额外的instructions。
- < smmintrin.h > : SSE 4.1, 支持点乘以及更多的整形操作。
- < nmmintrin.h > : SSE 4.2, 增加了额外的instructions。
- < immintrin.h > : AVX, 支持同时操作8个单精度浮点数或4个双精度浮点数。
每一个头文件都包含了之前的所有头文件,所以如果你想要使用SSE4.2以及之前SSE3, SSE2, SSE中的所有函数就只需要包含
命名规则
SSE/AVX提供的数据类型和函数的命名规则如下:
- 数据类型通常以_mxxx(T)的方式进行命名,其中xxx代表数据的位数,如SSE提供的__m128为128位,AVX提供的__m256为256位。T为类型,若为单精度浮点型则省略,若为整形则为i,如__m128i,若为双精度浮点型则为d,如__m256d。
- 操作浮点数的内置函数命名方式为:_mm(xxx)_name_PT。 xxx为SIMD寄存器的位数,若为128m则省略,如_mm_addsub_ps,若为_256m则为256,如_mm256_add_ps。 name为函数执行的操作的名字,如加法为_mm_add_ps,减法为_mm_sub_ps。 P代表的是对矢量(packed data vector)还是对标量(scalar)进行操作,如_mm_add_ss是只对最低位的32位浮点数执行加法,而_mm_add_ps则是对4个32位浮点数执行加法操作。 T代表浮点数的类型,若为s则为单精度浮点型,若为d则为双精度浮点,如_mm_add_pd和_mm_add_ps。
- 操作整形的内置函数命名方式为:_mm(xxx)_name_epUY。xxx为SIMD寄存器的位数,若为128位则省略。 name为函数的名字。U为整数的类型,若为无符号类型则为u,否在为i,如_mm_adds_epu16和_mm_adds_epi16。Y为操作的数据类型的位数,如_mm_cvtpd_pi32。
Intrinsics分类
instructions按执行操作类别的不同主要分为以下几类:
- 存取操作(load/store/set)
load系列可以用来从内存中载入数据到SSE/AVX提供的类型中,如:
void test()
{
__declspec(align(16)) float p[] = { 1.0f, 2.0f, 3.0f, 4.0f };
__m128 v = _mm_load_ps(p);
}
_mm_load_ps可以从16字节对齐的连续内存中加载4个32位单精度浮点数到__m128数据类型中(若不对齐则加载会出错)。
_mm_loadu_ps同_mm_load_ps的作用相同,但不要求提供的内存地址对齐。
_mm_load_ps1是从内存中载入一个32位浮点数,并重复存储到__m128中的4个浮点数中,即:m[0] = p[0], m[1] = p[0], m[2] = p[0], m[3] = p[0]。
_mm_load_ss则是从内存中载入一个32位浮点数,并将其赋值给__m128中的最低位的浮点数,并将高位的3个浮点数设置为0,即:m[0] = p[0], m[1] = 0, m[2] = 0, m[3] = 0。
_mm_loadr_ps位载入4个32位浮点数并将其反向赋值给__m128中的4个浮点数,即:m[0] = p[3], m[1] = p[2], m[2] = p[1], m[3] = p[0]。
除此之外还有_mm_loadh_pd,_mm_loadl_pi等…
store系列可以将SSE/AVX提供的类型中的数据存储到内存中,如:
void test()
{
__declspec(align(16)) float p[] = { 1.0f, 2.0f, 3.0f, 4.0f };
__m128 v = _mm_load_ps(p);
__declspec(align(16)) float a[] = { 1.0f, 2.0f, 3.0f, 4.0f };
_mm_store_ps(a, v);
}
_mm_store_ps可以__m128中的数据存储到16字节对齐的内存。
_mm_storeu_ps不要求存储的内存对齐。
_mm_store_ps1则是把__m128中最低位的浮点数存储为4个相同的连续的浮点数,即:p[0] = m[0], p[1] = m[0], p[2] = m[0], p[3] = m[0]。
_mm_store_ss是存储__m128中最低位的位浮点数到内存中。
_mm_storer_ps是按相反顺序存储__m128中的4个浮点数。
set系列可以直接设置SSE/AVX提供的类型中的数据,如:
__m128 v = _mm_set_ps(0.5f, 0.2f, 0.3f, 0.4f);
_mm_set_ps可以将4个32位浮点数按相反顺序赋值给__m128中的4个浮点数,即:_mm_set_ps(a, b, c, d) : m[0] = d, m[1] = c, m[2] = b, m[3] = a。
_mm_set_ps1则是将一个浮点数赋值给__m128中的四个浮点数。
_mm_set_ss是将给定的浮点数设置到__m128中的最低位浮点数中,并将高三位的浮点数设置为0.
_mm_setzero_ps是将__m128中的四个浮点数全部设置为0.
- 算术运算
SSE/AVX提供的算术运算操作包括:
- _mm_add_ps,_mm_add_ss等加法系列
- _mm_sub_ps,_mm_sub_pd等减法系列
- _mm_mul_ps,_mm_mul_epi32等乘法系列
- _mm_div_ps,_mm_div_ss等除法系列
- _mm_sqrt_pd,_mm_rsqrt_ps等开平方系列
- _mm_rcp_ps,_mm_rcp_ss等求倒数系列
- _mm_dp_pd,_mm_dp_ps计算点乘
此外还有向下取整,向上取整等运算,这里只列出了浮点数支持的算术运算类型,还有一些整形的算术运算类型未列出。
- 比较运算
SSE/AVX提供的比较运算操作包括:
- _mm_max_ps逐分量对比两个数据,并将较大的分量存储到返回类型的对应位置中。
- _mm_min_ps逐分量对比两个数据,并将较小的分量存储到返回类型的对应位置中。
- _mm_cmpeq_ps逐分量对比两个数据是否相等。
- _mm_cmpge_ps逐分量对比一个数据是否大于等于另一个是否相等。
- _mm_cmpgt_ps逐分量对比一个数据是否大于另一个是否相等。
- _mm_cmple_ps逐分量对比一个数据是否小于等于另一个是否相等。
- _mm_cmplt_ps逐分量对比一个数据是否小于另一个是否相等。
- _mm_cmpneq_ps逐分量对比一个数据是否不等于另一个是否相等。
- _mm_cmpnge_ps逐分量对比一个数据是否不大于等于另一个是否相等。
- _mm_cmpngt_ps逐分量对比一个数据是否不大于另一个是否相等。
- _mm_cmpnle_ps逐分量对比一个数据是否不小于等于另一个是否相等。
- _mm_cmpnlt_ps逐分量对比一个数据是否不小于另一个是否相等。
此外还有一些执行单分量对比的比较运算
- 逻辑运算
SSE/AVX提供的逻辑运算操作包括:
- _mm_and_pd对两个数据逐分量and
- _mm_andnot_ps先对第一个数进行not,然后再对两个数据进行逐分量and
- _mm_or_pd对两个数据逐分量or
- _mm_xor_ps对两个数据逐分量xor
- Swizzle运算
包含_mm_shuffle_ps,_mm_blend_ps, _mm_movelh_ps等。
这里主要介绍以下_mm_shuffle_ps:
void test()
{
__m128 a = _mm_set_ps(1, 2, 3, 4);
__m128 b = _mm_set_ps(5, 6, 7, 8);
__m128 v = _mm_shuffle_ps(a, b, _MM_SHUFFLE(1, 0, 3, 2)); // 2, 1, 8, 7
}
_mm_shuffle_ps读取两个__m128类型的数据a和b,并按照_MM_SHUFFLE提供的索引将返回的__m128类型数据的低两位设置为a中按索引值取得到的对应值,将高两位设置为按索引值从b中取得到的对应值。索引值在0到3之间,分别以相反的顺序对应__m128中的四个浮点数。
SSE/AVX还提供了类型转换等操作,这里就不做介绍了。
PS:补充一个操作指令:_mm_cvtss_f32,可以获取__m128中的最低位浮点数并返回。
相关资料信息查询
文中先关测试和介绍 暂时先以手头台式机的Intel i5 8500 X86架构CPU为例,其他的处理器可自行扩展。
可以通过该链接去查看自己的处理器支持那些SIMD指令集,我的i5 8500支持Intel® SSE4.1, Intel® SSE4.2, Intel® AVX2,这里的指令集是不断扩展的,也就是说同时也支持以前的SIMD指令集,如SSE3,SSE2,MMX等。
SSE/AVX的API可以参考: Intel® Intrinsics Guide
实测环节
这边文章先简单测试下性能对比,后续针对深度学习的算子优化,慢慢再优化和测试。先贴测试代码:
#include <iostream>
#include <random>
#include <ctime>
#include <vector>
#include <chrono>
#include <emmintrin.h>
using namespace std;
#define TIME_STAMP_START(name) auto time_start_##name = std::chrono::steady_clock::now();
#define TIME_STAMP_END(name) \
{ \
auto time_end_##name = std::chrono::steady_clock::now(); \
auto time_cost = std::chrono::duration<double, std::milli>(time_end_##name - time_start_##name).count(); \
std::cout << #name " Time Cost # " << time_cost << " ms ---------------------" << std::endl; \
}
void tpd_vsadd_normal(const float* x, const float* y, float* z, int n) {
int i = 0;
for (i = 0; i < n; i++) {
z[i] = x[i] + y[i];
}
}
void tpd_vsadd_ptr(const float* x, const float* y, float* z, int n) {
int blocks = n;
while (blocks > 0U) {
*(z++) = (*(x++)) + (*(y++));
/* Decrement the loop counter */
blocks--;
}
}
void tpd_vsadd_sse(const float* x, const float* y, float* z, int n) {
int blocks;
/*loop Unrolling */
blocks = n >> 2U;
while (blocks > 0U) {
_mm_storeu_ps(z, _mm_add_ps(_mm_loadu_ps(x), _mm_loadu_ps(y)));
x += 4;
y += 4;
z += 4;
/* Decrement the loop counter */
blocks--;
}
/* If the blockSize is not a multiple of 4, compute any remaining output samples here.
** No loop unrolling is used. */
blocks = n % 0x4U;
while (blocks > 0U) {
(*z++) = (*x++) + (*y++);
/* Decrement the loop counter */
blocks--;
}
}
int main()
{
uniform_real_distribution<float> u(-100, 100);
default_random_engine e(time(NULL));
int n = 10000000;
vector<float> a(n);
vector<float> b(n);
vector<float> c(n);
for (size_t i = 0; i < n; i++)
{
a[i] = u(e);
b[i] = u(e);
}
TIME_STAMP_START(NO_SSE)
tpd_vsadd_sse(a.data(),b.data(),c.data(),n);
TIME_STAMP_END(NO_SSE)
return 0;
}
tpd_vsadd_normal()函数为通过数组索引下标访问数据计算,tpd_vsadd_ptr()是通过指针访问,tpd_vsadd_sse()则是通过SIMD指令进行计算。前两个函数作为第三个函数的对比,便于分析。
这里有个小知识点,通过指针访问数据会比通过数组索引下标访问效率高,在下面的测试过程中也有体现。其原因我们可以通过查看对应的反汇编代码进行分析:
索引下标访问:
0000000000001309 <_Z16tpd_vsadd_normalPKfS0_Pfi>:
1309: f3 0f 1e fa endbr64
130d: 55 push %rbp
130e: 48 89 e5 mov %rsp,%rbp
1311: 48 89 7d e8 mov %rdi,-0x18(%rbp)
1315: 48 89 75 e0 mov %rsi,-0x20(%rbp)
1319: 48 89 55 d8 mov %rdx,-0x28(%rbp)
131d: 89 4d d4 mov %ecx,-0x2c(%rbp)
1320: c7 45 fc 00 00 00 00 movl $0x0,-0x4(%rbp)
1327: c7 45 fc 00 00 00 00 movl $0x0,-0x4(%rbp)
132e: eb 50 jmp 1380 <_Z16tpd_vsadd_normalPKfS0_Pfi+0x77>
1330: 8b 45 fc mov -0x4(%rbp),%eax
1333: 48 98 cltq
1335: 48 8d 14 85 00 00 00 lea 0x0(,%rax,4),%rdx
133c: 00
133d: 48 8b 45 e8 mov -0x18(%rbp),%rax
1341: 48 01 d0 add %rdx,%rax
1344: f3 0f 10 08 movss (%rax),%xmm1
1348: 8b 45 fc mov -0x4(%rbp),%eax
134b: 48 98 cltq
134d: 48 8d 14 85 00 00 00 lea 0x0(,%rax,4),%rdx
1354: 00
1355: 48 8b 45 e0 mov -0x20(%rbp),%rax
1359: 48 01 d0 add %rdx,%rax
135c: f3 0f 10 00 movss (%rax),%xmm0
1360: 8b 45 fc mov -0x4(%rbp),%eax
1363: 48 98 cltq
1365: 48 8d 14 85 00 00 00 lea 0x0(,%rax,4),%rdx
136c: 00
136d: 48 8b 45 d8 mov -0x28(%rbp),%rax
1371: 48 01 d0 add %rdx,%rax
1374: f3 0f 58 c1 addss %xmm1,%xmm0
1378: f3 0f 11 00 movss %xmm0,(%rax)
137c: 83 45 fc 01 addl $0x1,-0x4(%rbp)
1380: 8b 45 fc mov -0x4(%rbp),%eax
1383: 3b 45 d4 cmp -0x2c(%rbp),%eax
1386: 7c a8 jl 1330 <_Z16tpd_vsadd_normalPKfS0_Pfi+0x27>
1388: 90 nop
1389: 90 nop
138a: 5d pop %rbp
138b: c3 ret
指针访问:
000000000000138c <_Z13tpd_vsadd_ptrPKfS0_Pfi>:
138c: f3 0f 1e fa endbr64
1390: 55 push %rbp
1391: 48 89 e5 mov %rsp,%rbp
1394: 48 89 7d e8 mov %rdi,-0x18(%rbp)
1398: 48 89 75 e0 mov %rsi,-0x20(%rbp)
139c: 48 89 55 d8 mov %rdx,-0x28(%rbp)
13a0: 89 4d d4 mov %ecx,-0x2c(%rbp)
13a3: 8b 45 d4 mov -0x2c(%rbp),%eax
13a6: 89 45 fc mov %eax,-0x4(%rbp)
13a9: eb 38 jmp 13e3 <_Z13tpd_vsadd_ptrPKfS0_Pfi+0x57>
13ab: 48 8b 45 e8 mov -0x18(%rbp),%rax
13af: 48 8d 50 04 lea 0x4(%rax),%rdx
13b3: 48 89 55 e8 mov %rdx,-0x18(%rbp)
13b7: f3 0f 10 08 movss (%rax),%xmm1
13bb: 48 8b 45 e0 mov -0x20(%rbp),%rax
13bf: 48 8d 50 04 lea 0x4(%rax),%rdx
13c3: 48 89 55 e0 mov %rdx,-0x20(%rbp)
13c7: f3 0f 10 00 movss (%rax),%xmm0
13cb: f3 0f 58 c1 addss %xmm1,%xmm0
13cf: 48 8b 45 d8 mov -0x28(%rbp),%rax
13d3: 48 8d 50 04 lea 0x4(%rax),%rdx
13d7: 48 89 55 d8 mov %rdx,-0x28(%rbp)
13db: f3 0f 11 00 movss %xmm0,(%rax)
13df: 83 6d fc 01 subl $0x1,-0x4(%rbp)
13e3: 83 7d fc 00 cmpl $0x0,-0x4(%rbp)
13e7: 75 c2 jne 13ab <_Z13tpd_vsadd_ptrPKfS0_Pfi+0x1f>
13e9: 90 nop
13ea: 90 nop
13eb: 5d pop %rbp
13ec: c3 ret
通过指针访问数组元素会比通过下标索引访问数组效率高很多的原因,从汇编代码中可以看出,通过数组索引下标去访问,由于i的变化,每次循环需要以base + i * offset的方式重新计算并加载下标值,然后再取值;对于使用指针访问数组元素来说,在计算过程中已经不断的偏移到当前要使用的指针,即访问当前指针只需要cur_ptr = pre_ptr + 4。可以使用 https://godbolt.org/ 工具对比查看源码和汇编代码,其中操作步骤还会对应标记颜色,十分方便。
执行效率结果对比:
zhengjian@zhengjian-VirtualBox:~/workspace/code/test$ ./test111
tpd_vsadd_normal Time Cost # 24.6219 ms ---------------------
zhengjian@zhengjian-VirtualBox:~/workspace/code/test$ ./test111
tpd_vsadd_ptr Time Cost # 20.2514 ms ---------------------
zhengjian@zhengjian-VirtualBox:~/workspace/code/test$ ./test111
tpd_vsadd_sse Time Cost # 11.8113 ms ---------------------
这个对比结果,对于第一次接触SIMD的我来说十分震惊,可以看出通过SIMD指令集进行并行计算,相对于普通的下标访问计算可以提升一倍的计算速度。同时可以看出通过指针访问的速度要比数组索引下标访问速度快很多。对于使用CPU进行数据密集型计算的场景来说,SIMD值得进行深入探究。
参考
- https://teapoly.github.io/tech/2021/01/02/simd-for-vector-add.html
- https://zhuanlan.zhihu.com/p/416172020
- https://zhuanlan.zhihu.com/p/55327037
文档信息
- 本文作者:JianZheng
- 本文链接:https://zhengjian526.github.io/left-handed_knife//2023/03/18/SIMD-Intel-SSE-and-AVX/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)